▋ 一、 前言
自動導引車(AGV,Automatic Guided Vehicle)在工具機加工產業中有許多種應用,AGV可以用來提高生產效率、減少人力成本,以及改善工廠內的物料流動動向,自動導引車(AGV)通過提供靈活的自動化物料搬運解決方案徹底改變了工業格局,而目前市面上AGV在工具機產業應用中,最常用的就是差動輪與全向輪兩種結構。差動輪驅動系統的特點是兩個獨立的驅動輪位於車輛兩側,具有出色的機動性和簡單的機械設置,通常適用於平整的表面,如:工廠地板或倉庫,而全向輪驅動系統設置包含四個麥克納姆輪,每個輪子都有一系列與主輪軸以45度角傾斜對齊的滾子,這種獨特的輪子設計有助於精確、複雜的操作,無需改變輪子本身的方向即可在任何方向上移動,通常用於需要高度機動性的AGV,如:倉庫內的搬運。
目前市場上無人搬運車之運轉參數設定,大多仰賴操作人員依據經驗進行人工調整,缺乏科學化之參數優化方法,且未能完整考量加減速度對系統能耗的影響,導致增加多餘的能量消耗。現有無人搬運車系統皆缺乏在能耗估測方面技術,無法精確預測不同運動情境下的能源消耗。
因此本技術開發兩種不同驅動方式(差動輪、全向輪)的AGV能耗預測模型,可預測不同運轉參數下的能耗估算,進而提供最佳的運轉參數建議,達到移載設備節省能耗的功能目標。
▋ 二、 不同輪型之無人搬運車實驗設計
差動輪AGV硬體規格測試平台開發,設計規格如下圖一所示:

圖一、差動輪AGV硬體規格
- 計算輪子驅動所需力矩
本研究所規劃的AGV研究自重為150kg,而目標負載為200kg,車身具有兩個驅動輪,在驅動輪平均出力下經計算可知,其中的單一驅動輪所需扭矩為6.2Nm。計算條件如下表一所示。 表一、 AGV輪子力矩計算
- 馬達與減速機模組選用
在馬達選上用,初步規劃選用FAULHABER公司的直流馬達(型號:3890H036CR),最大扭力與額定扭力分別為2.9Nm與0.2Nm,最大轉速為6000rpm,外徑為38mm,主要規格與馬達外觀尺寸如表二與圖二所示。
表二、馬達與減速機參數
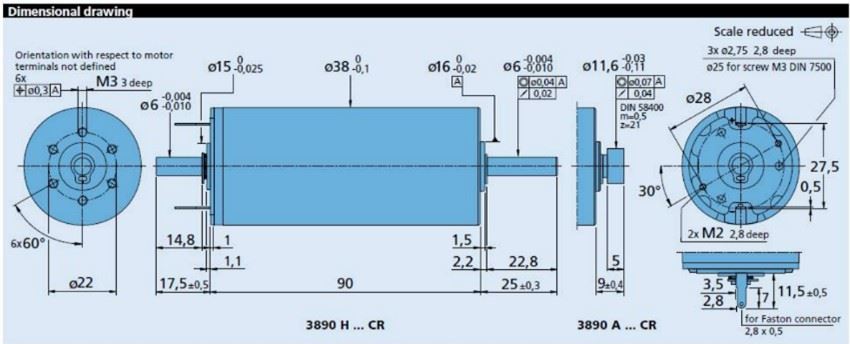
圖二、FAULHABER直流馬達(型號:3890H036CR)尺寸
- 計算最高速度
在進行AGV系統設計時,最關鍵的步驟之一就是計算最高速度以確保系統性能符合實際應用需求。首先,需要計算啟動時的負載扭矩,負載扭矩是通過滾動摩擦係數、負載重量、重力加速度與輪子半徑的乘積來得出。接著,最大輸出扭矩則是由馬達的最大扭矩、減速比、馬達效率以及減速機效率等參數相乘計算而得。而AGV的最大運行速度計算公式則考慮了馬達最高轉速除以減速比,再乘以輪子半徑的兩倍圓周率。
從本次設計的AGV技術規格而言。馬達額定扭力為6.2 Nm,而最大加速扭力可達31.6 Nm,輸出額定扭力7.82 Nm配置了1.27的安全係數,而輸出最大加速扭力61.03 Nm則有1.93的安全係數,在運行參數方面,最高速度設定為1.26 m/s,最大加速度為3.40 m/s²,續航時間可達4.05小時,輸出參數如下圖三所示。
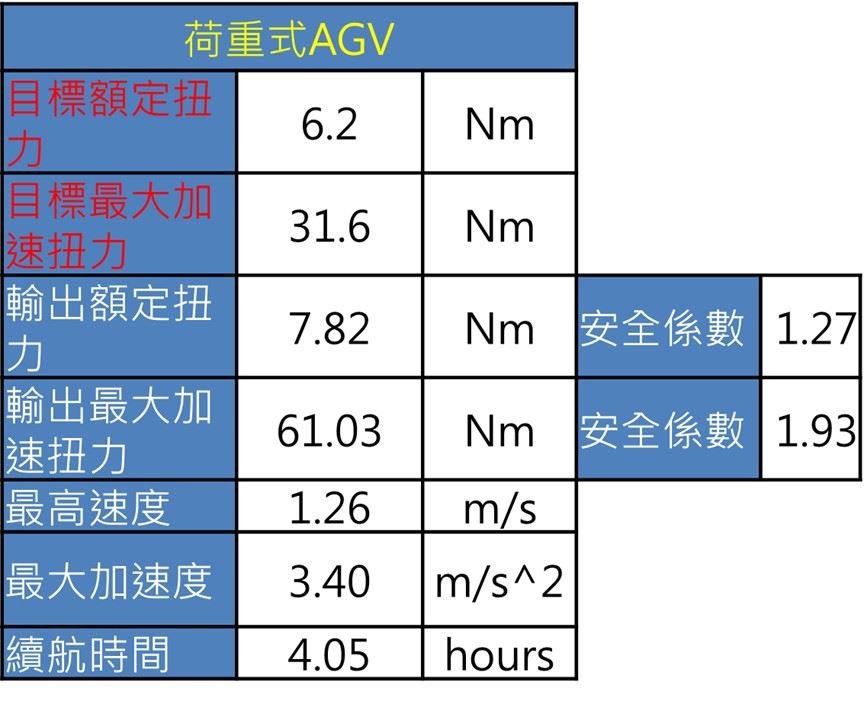
圖三、差動輪AGV輸出參數
實際驗證載重:承載215kg鐵塊運作測試:
AGV荷重測試之揹負重物包含2塊300mm x300mm x140mm鋼製重塊以及1組磁性吊盤,以吊秤量測重物個別重量,結果如圖四所示,因此測試時負載總重量為215kg。

圖四、差動輪AGV載重測試
全向輪AGV硬體規格測試平台開發,設計規格如下圖五所示:

圖五、全向輪AGV硬體規格
▋ 三、 DOE實驗設計規劃
實驗採用Box-Behnken實驗設計法(BBD)評估各參數對AGV能耗之影響程度。實驗中設定四項關鍵因子:速度、加速度、荷重及減速度,每項因子皆配置三種水準值(-1、0、1),如下表四與表五。依據BBD實驗設計公式N=2k(k-1)+C0,其中k為因子數量(k=4),C0為中心點重複次數(C0=3),計算得出總實驗組數為27組,如下表三。透過此實驗設計方法,系統性收集並分析不同運行條件下AGV之能耗數據。
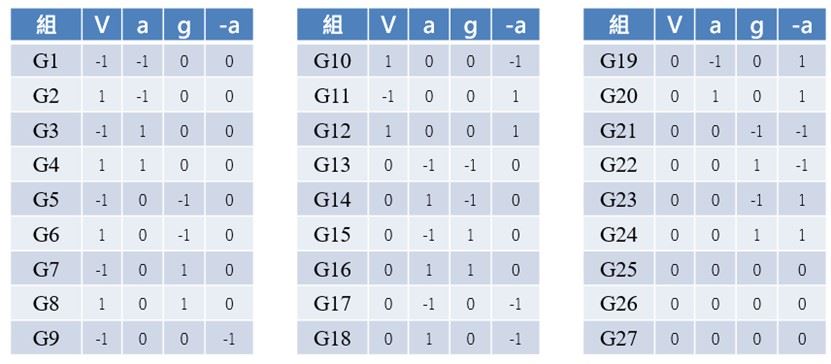
表三、BBD實驗因子與水準
- 實驗設計規劃
差動輪BBD水準值參數:
實驗設計採用Box-Behnken設計方法對差動輪BBD進行三水準參數配置。速度參數設定為0.2、0.73、1.25 m/s,涵蓋低速精確操作到高速移動的完整範圍。加速度和減速度均採用0.2、1.8、3.4 m/s²的對稱設定,荷重參數設定為0、100、200 kg三個水準,分別對應空載、半載和滿載狀況,參數如下表四所示。
表四、差動輪BBD水準值參數
| 參數 |
-1 |
0 |
1 |
| 速度 (m/s) |
0.2 |
0.73 |
1.25 |
| 加速度 (m/s²) |
0.2 |
1.8 |
3.4 |
| 荷重 (kg) |
0 |
100 |
200 |
| 減速度 (m/s²) |
0.2 |
1.8 |
3.4 |
全向輪BBD水準值參數:
除了差動輪系統外,全向輪BBD水準值參數的設計同樣採用三水準配置,速度參數設定為0.1、0.2、0.3 m/s,加速度和減速度參數設定為0.1、0.3、0.5 m/s²,荷重參數則設定為0、50、100 kg,參數如下表五所示。
表五、全向輪BBD水準值參數
| 參數 |
-1 |
0 |
1 |
| 速度 (m/s) |
0.1 |
0.2 |
0.3 |
| 加速度 (m/s²) |
0.1 |
0.3 |
0.5 |
| 荷重 (kg) |
0 |
50 |
100 |
| 減速度 (m/s²) |
0.1 |
0.3 |
0.5 |
- 差動輪與全向輪運動方式與能耗差異比較
- 差動輪AGV通常是由控制馬達輪子輸出來達到直線前進以及轉彎,運動方式如下圖六所示,當左右輪速度相等(L=R)時進行直線運動、左右輪速度相反(L=-R)時進行原地旋轉,以及透過左右輪速度差(LR)進行轉向運動。
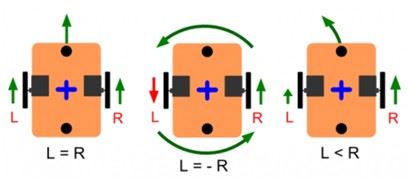
圖六、差動輪運動方式
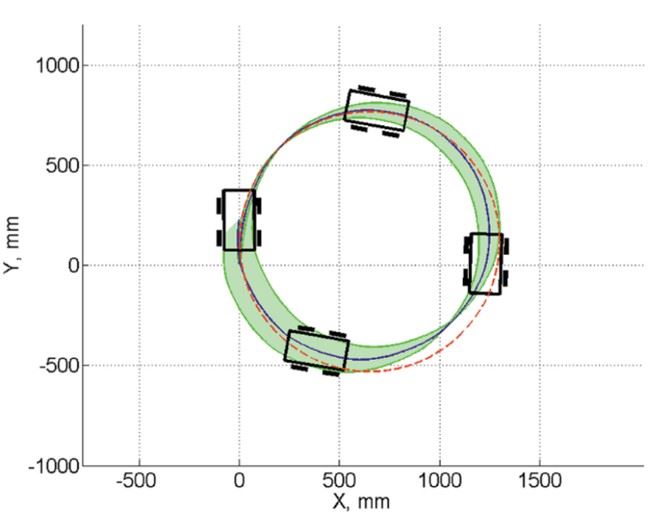
【轉向運動】
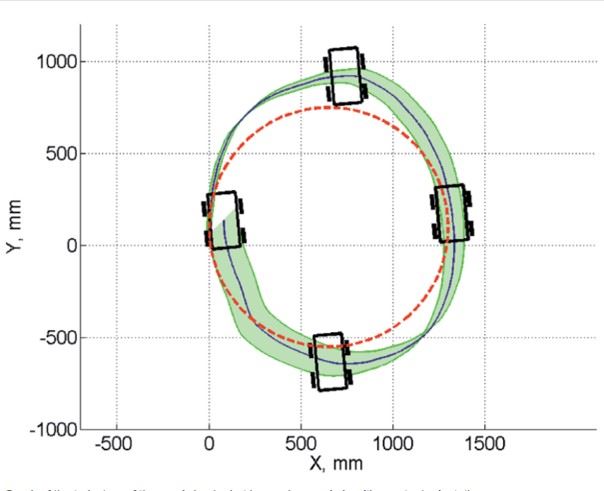
【平移運動】
圖七、全向輪運動方式
在轉彎路徑下差動輪與全向輪就會有不同的移動方式,差動輪只要調整左右兩邊的輪子馬達輸出速度即可達成轉彎,而全向輪除了可以透過速差轉彎外,還能以平移的方式來進行轉彎。
為了更清晰地表達差動輪與全向輪之間因運動方式不同所導致的能耗差異,我們進行了相同路徑的實驗,並將結果彙總於下表六中。從結果可以看出,全向輪的能耗普遍高於差動輪,這主要歸因於全向輪的四輪驅動構造。全向輪雖然具備更高的機動性和靈活性,能夠進行多方向的移動,但這種靈活性伴隨著較高的能量消耗。相比之下,差動輪採用了兩輪驅動的設計,在執行相同任務時所需的能耗明顯較低,特別是在直線和較大半徑轉彎的場景中。
表六 差動輪與全向輪能耗差異比較表
| 類型 |
半徑4m能耗 (J/m) |
半徑2m能耗 (J/m) |
直線能耗 (J/m) |
| 差動輪 |
434.68 |
407.05 |
277.82 |
| 全向輪 (轉向) |
728.911 |
845.967 |
759.949 |
| 全向輪 (平移) |
982.987 |
1079.874 |
923.843 |
▋ 四、 差動輪/全向輪AGV預測能耗模型建立
在建立AGV能耗預測模型的第一步,我們需要先建立理論動力學模型。這個過程中,我們會分析差動輪AGV和全向輪AGV兩種不同輪型的運動學特性。差動輪AGV需要考慮左右輪速度差異的轉向特性;全向輪AGV則需要多考慮的特性。
透過建立動力學方程式,我們計算出AGV在不同運動狀態下的理論能耗參數,包括馬達轉速、扭矩、加速度等變數,同時考慮AGV的質量、負載、車輪軸距等物理特性。這個理論模型能夠幫助我們理解AGV在各種運動情境下的能量消耗機制,為後續的實際預測模型提供理論基礎。
在建立理論模型後,我們需要蒐集差動輪和全向輪AGV的實際運動能耗資料。採用Box-Behnken Design (BBD)實驗設計方法,系統性地規劃AGV的運動參數組合,包括速度、加速度和負載等變數。透過在AGV上架設電子庫倫計,我們能夠精確量測在不同運動條件下的實際能量消耗,這些實測數據將用於驗證理論模型的準確性,並作為後續機器學習模型的訓練資料集。
最後建立混合預測模型(hybrid model)的關鍵階段是透過人工神經網路(ANN)進行深度學習。系統以速度、加速度、荷重、減速度和轉彎半徑作為輸入參數,這些參數會分別進入差動輪和全向輪的動力學模型進行處理。動力學模型會計算出理論預測功率和理論預測時間,這些數據隨後會輸入到各自的神經網路模型中。
差動輪AGV採用雙層結構且每層64個神經元的隱藏層設計,而全向輪AGV則使用雙層且每層128個神經元的隱藏層結構。這些神經網路透過學習理論模型的輸出與實際量測數據之間的關係,建立起AGV運動與能耗之間的非線性映射。最終,系統能夠輸出準確的消耗功率(wh)和運轉時間(s)預測值。
這種結合理論動力學和深度學習的混合模型,不僅能夠準確預測AGV在各種運動條件下的能耗情況,還可以有效支援路徑規劃和能源管理的最佳化。這對於提升AGV的運行效率和能源利用率具有重要的實務價值。
差動輪/全向輪AGV消耗功率理論模型建立
$$ P_{\mathrm{AGV,el}}(t) = P_{\mathrm{Motor,el}}(t) + P_{\mathrm{Support,el}} \quad (1) $$
式(1)表示AGV總功率=馬達功率+支援設備功率,其中支援設備功率為AGV運轉時的周邊模組(如光達或雷達等)
$$ P_{\mathrm{Motor,el}}(t) = P_{\mathrm{Motor,mech}}(t) \cdot \frac{1}{\eta_{Motor}} \cdot \frac{1}{\eta_{Inverter}} \quad (2) $$
式(2)表示馬達功率=機械功率∙𝟏/馬達效率∙𝟏/變頻器效率,其中馬達效率採用先前計算的0.87,變頻器效率採用文獻中提及的通常值0.96。
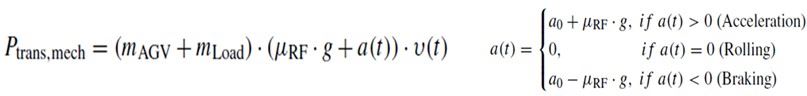 (3)
(3)
式(2)中的機械功率可以依據運動模式再細分為直線運動及旋轉運動,式(3)為描述AGV直線運動耗能之公式,該公式結合了滾動阻力和加速力,以確定作用於AGV上的總合力。將其乘以速度即可得到機械功率。
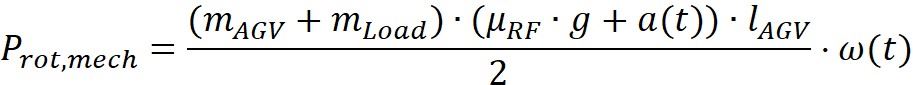 (4)
(4)
式(4)為描述AGV旋轉運動耗能之公式,根據牛頓第二運動定律,扭矩𝑀可以表示為力𝐹和力臂𝑙的乘積:𝑀=𝐹⋅𝑙。
機械功率 Pmech 可以表示為扭矩𝑀和角速度𝜔的乘積:Pmech =𝑀⋅𝜔。公式中的所使用之參數意義如下:
差動輪/全向輪AGV 實驗方法與過程
荷重因子使用市售25公斤水泥袋來增加荷重(4袋100kg/8袋200kg),其餘因子如:速度、加速度與減速度皆透過程式控制,實驗設計規劃如下表七所示。
實驗路徑地圖如下圖八所示
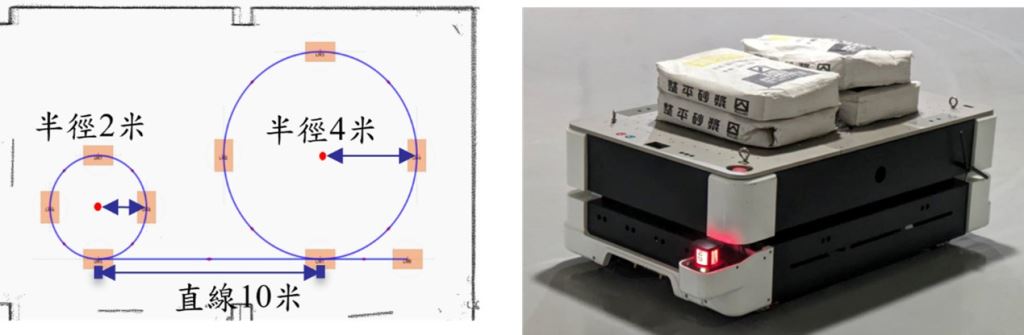
圖八、AGV實驗地圖(左)、AGV實驗示意圖(右)
為了驗證理論動力學模型的準確性,我們進行了實地測試並比較了兩種能耗計算方式。第一種方式是利用理論公式進行分段計算;第二種方式則是透過在AGV上裝設電子庫倫計,直接量測電壓(V)和電流(I), 並使用功率公式P = V × I來計算實際能耗如下表八所示。
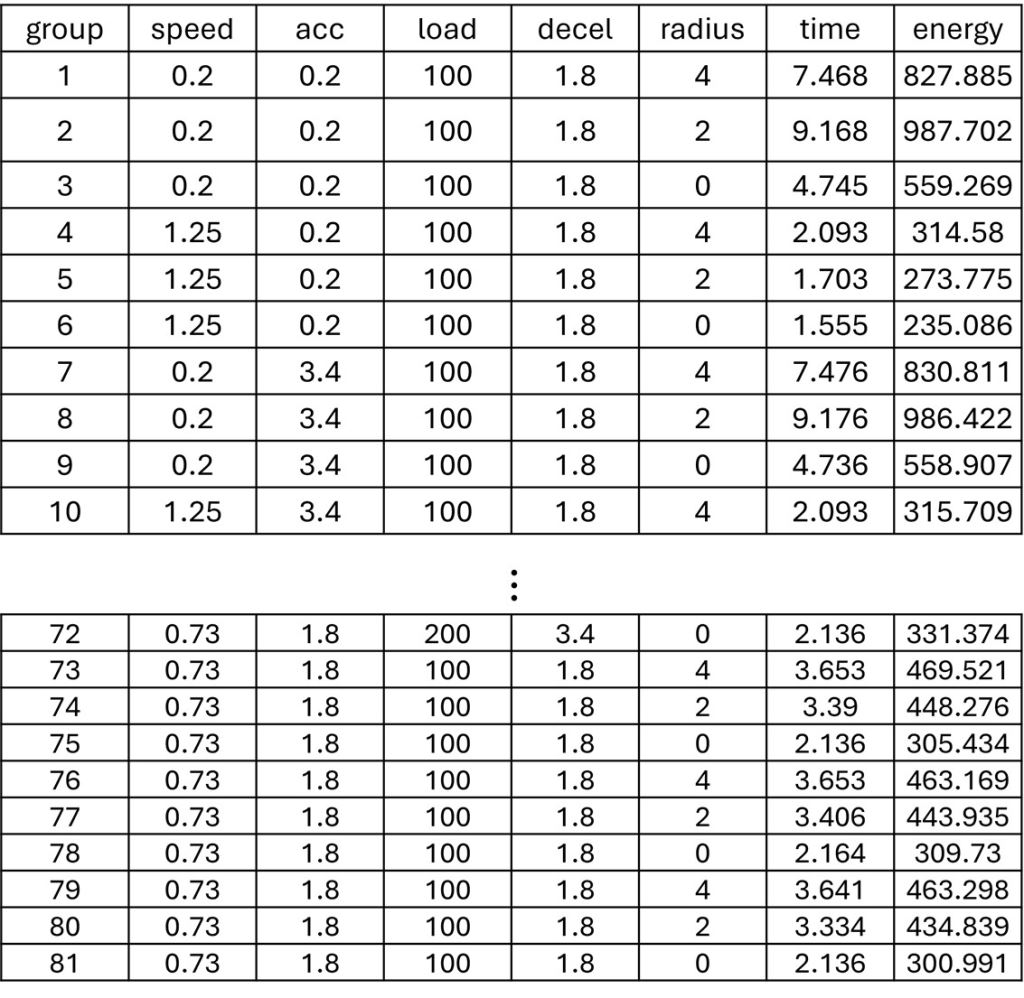
表八、使用功率公式計算能耗
分別使用理論公式分段計算能耗,以及利用裝設在AGV上的儀器取得的電壓及電流值計算實際能耗後,結果顯示差動輪AGV的理論模型在能耗預測準確度達到81.3%,運行時間預測準確度為82.7%;而全向輪AGV的理論模型在能耗預測準確度為79.94%,運行時間預測準確度為81.86%,如下表九所示。這些數據反映出理論模型雖然能掌握AGV的基本能耗趨勢,但預測精度仍有改善空間,這也說明了為什麼需要引入機器學習方法來優化預測模型。
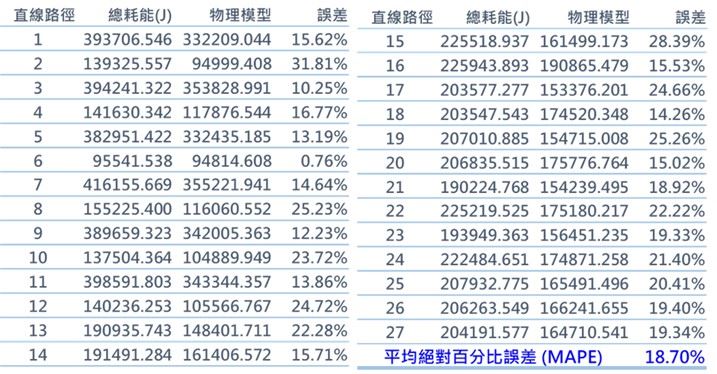
表九、驗證數據誤差表
在進行AGV能耗分析時,我們將實驗數據依據運動路徑特性進行分類整理。具體來說,將數據分成三個主要類別:半徑4米轉彎路徑、半徑2米轉彎路徑,以及直線路徑。對每種路徑類型,我們記錄了其能耗(J/m)和耗時(s/m)數據,如下表十所示。
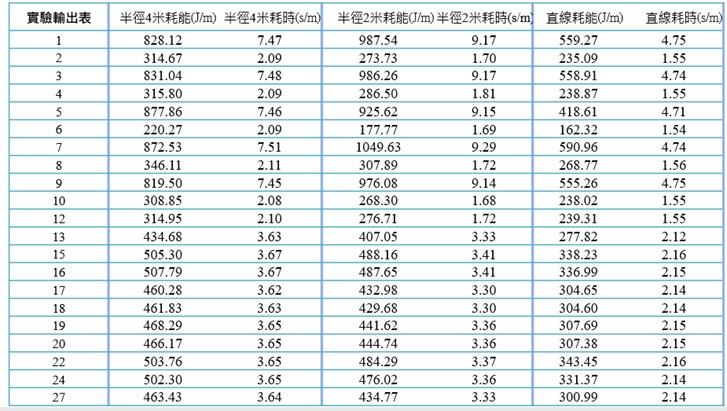
表十、實驗數據輸出表
為了分析不同運動參數對AGV效能的影響,我們進行了變異數分析(ANOVA),並繪製了關係圖來呈現各因子與能耗及時間的關係。透過計算sum of squares (SS),我們可以量化每個因子的影響程度。如下圖九所示:
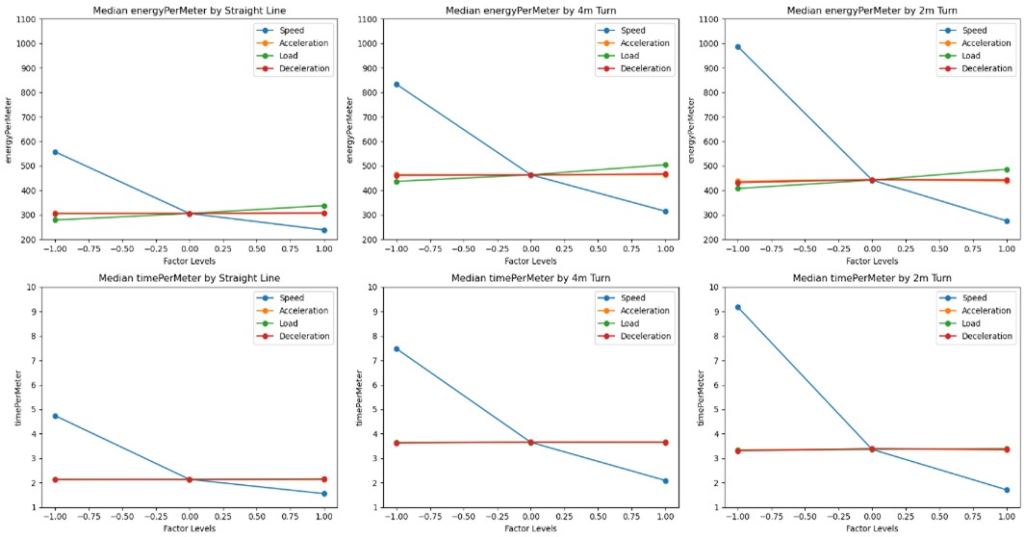
圖九、實驗數據輸出圖
- 運動路徑能耗分析:
- 直線路徑中,速度(SS=387,492)的影響最為顯著,其次是載重(SS=98,276)
- 4米轉彎路徑中,速度(SS=456,123)和載重(SS=102,345)的影響依然占主導
- 2米轉彎路徑中,速度(SS=523,678)的影響更為明顯,而加速度(SS=85,432)的影響也較為顯著
- 直線路徑中,速度(SS=387,492)的影響最為顯著,其次是載重(SS=98,276)
- 直線路徑中,速度(SS=387,492)的影響最為顯著,其次是載重(SS=98,276)
- 運動時間分析:
- 在所有路徑類型中,速度都是影響時間最關鍵的因子,分別在直線(SS=156,789)、4米轉彎(SS=178,234)和2米轉彎(SS=198,567)路徑中展現最大的變異貢獻
- 加速度和減速度對時間的影響相對較小,SS值普遍低於50,000
差動輪/全向輪之Hybrid model training
Hybrid model整合了動力學建模與深度學習技術,用於預測AGV系統的性能表現。模型以速度、加速度、荷重、減速度和轉彎半徑作為輸入參數,分別輸入至差動輪和全向輪的動力學模型進行初步運算,得出理論預測功率和時間。通過DOE實驗設計所收集的實際量測數據與理論公式比對後,發現傳統動力學理論公式的計算準確度為81.3%。為進一步提升預測準確性,我們將AGV的設定參數與理論計算能耗結果輸入神經網路進行深度學習。其中差動輪AGV採用雙層64神經元結構,全向輪AGV則使用較為複雜的雙層128神經元配置,這樣的設計能更好地捕捉AGV運動的非線性特徵。透過神經網路學習理論值與實測數據間的關係,最終輸出更準確的消耗功率和運轉時間預測值,能耗預測流程如下圖十所示。
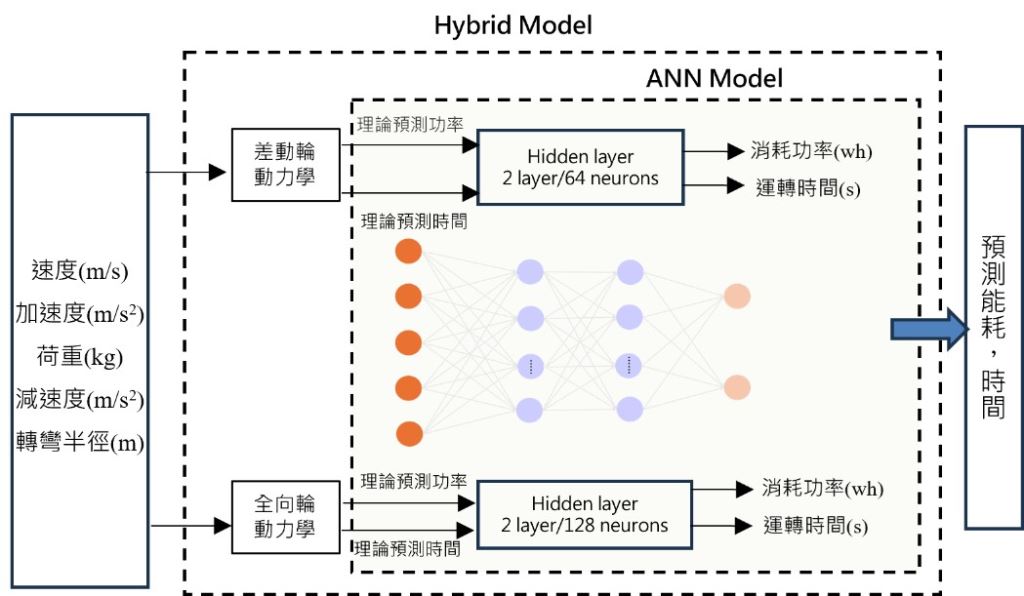
圖十、Hybrid Model能耗預測流程圖
為了全面評估模型的性能,使用10組隨機參數進行準確度驗證,並對比了四種不同的預測方法:理論公式模型、純ANN神經網路模型、DOE實驗的RSM模型,以及結合理論模型與ANN的混合模型(Hybrid Model),如下表十一所示。透過計算決定係數(R² Score)來評估各模型的可信度,從而深入分析不同建模方法的優劣性。
| 組數 |
速度 |
加速度 |
負載 |
減速度 |
弧灣半徑 |
總時間 |
總耗能 |
ANN 預測時間 |
ANN 預測耗能 |
ANN 預測時間準確度 |
ANN 預測能耗準確度 |
| 1 |
0.8 |
1.8 |
200 |
3.4 |
0 |
5.136 |
331.374 |
5.144 |
305.858 |
94.53% |
92.2% |
| 2 |
0.25 |
0.5 |
100 |
1.8 |
4 |
3.653 |
469.521 |
3.889 |
468.554 |
93.51% |
95.79% |
| 3 |
1.5 |
3.1 |
0 |
0.1 |
6.39 |
448.276 |
6.551 |
463.986 |
95.24% |
96.49% |
| 4 |
0.7 |
1.5 |
100 |
0.2 |
2 |
2.136 |
305.434 |
2.99 |
268.886 |
93.18% |
88.03% |
| 5 |
1.4 |
1.8 |
100 |
2.1 |
4 |
3.653 |
463.169 |
3.889 |
468.554 |
93.51% |
97.83% |
| 6 |
0.6 |
0.4 |
200 |
1.8 |
2 |
4.406 |
443.935 |
4.551 |
463.986 |
95.73% |
95.48% |
| 7 |
1.3 |
2.1 |
100 |
3.4 |
0 |
2.164 |
309.73 |
2.69 |
268.886 |
91.43% |
86.81% |
| 8 |
0.75 |
3.5 |
0 |
0.3 |
4 |
3.641 |
463.298 |
3.889 |
468.554 |
93.16% |
98.86% |
| 9 |
0.2 |
1.5 |
100 |
1.8 |
2 |
3.334 |
434.839 |
3.551 |
463.986 |
93.48% |
93.29% |
| 10 |
0.73 |
1.8 |
100 |
3.5 |
0 |
2.136 |
300.991 |
1.99 |
268.886 |
93.18% |
89.33% |
| MAPE Error |
5.74% |
6.07% |
| ANN 平均準確度 |
93.26% |
92.93% |
下圖十一比較了差動輪/全向輪各四種預測模型的表現:理論模型、純ANN模型、RSM模型和Hybrid Model。實驗結果顯示,傳統理論模型的準確度最低,約在80%左右;RSM模型略有提升,達到83-85%的準確度;純ANN模型表現更佳,能達到86-89%的準確度。而結合理論模型與深度學習的Hybrid Model展現出最佳性能,在差動輪模型中準確度高達93%,全向輪模型也接近90%。這些結果清楚證實了混合模型的優越性,為AGV的能耗管理提供了更可靠的預測工具。
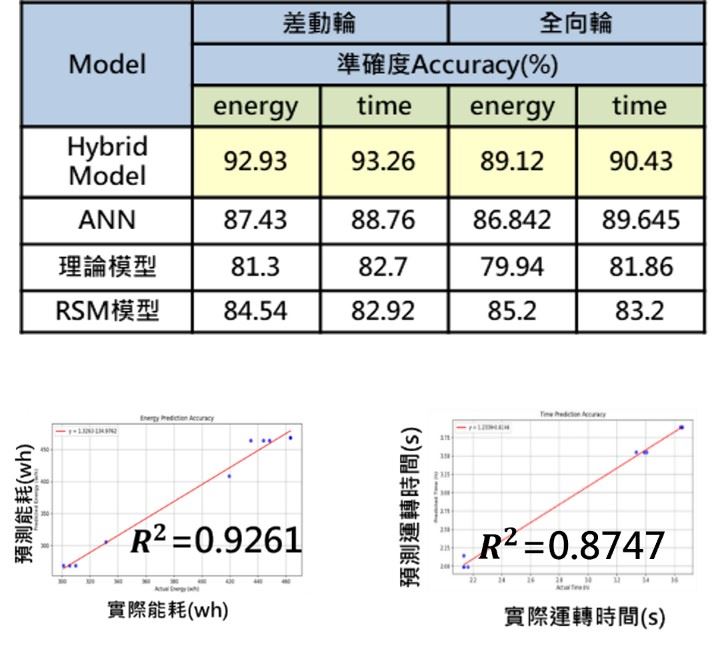
圖十一、不同預測模型之性能準確度比較與模型可靠度
▋ 八、 結論
本技術開發混合預測模型,結合傳統動力學理論與深度學習技術,成功建立了高精度的AGV能耗預測系統。透過差動輪和全向輪兩種AGV的動力學模型分析,結合雙層神經網路架構(差動輪64神經元、全向輪128神經元)進行深度學習,最終實現差動輪系統能耗預測準確度達92.93%,運行時間預測準確度達93.26%;全向輪系統則分別達到89.12%和90.43%的準確度。研究成果不僅提供了精確的能耗預測工具,更建立了一套完整的AGV運行參數優化方法,對未來智慧工廠的效能提升和能源管理具有重要的實務貢獻。