▋ 前言
馬達減速機在機械傳動系統中是不可或缺的,主要功能是將電動馬達的高轉速轉換為較低的轉速,以提高輸出扭矩,在這個過程中不僅能提高機械裝置的運作效率,還能增強負載能力,從而滿足不同工業應用的需求。一般常見的減速機主要使用齒輪機構,而行星齒輪系又因其高效能且緊湊的設計而受到青睞。如圖一所示,行星齒輪系通常由一個太陽齒輪、一個或多個環繞的行星齒輪、行星臂架以及外部的環齒輪組成。聚合物齒輪因為在輕量化、抗腐蝕性和噪音控制方面具有顯著優勢,因此在現代工程中正逐漸獲得關注。通常由各種塑料材料如聚甲醛(POM)、尼龍(PA)等製成,在降低重量的同時提供良好的機械性能,與傳統金屬齒輪相比,聚合物齒輪具有自潤滑的特性,減少了摩擦和磨損,延長了使用壽命。

圖一、行星齒輪系
齒輪強度分析是齒輪設計中很重要的一環,包含了齒面接觸應力與齒根彎曲應力的評估,齒輪強度與選擇的材料息息相關,因為計算較複雜,常藉由齒輪設計軟體輔助計算,但是因為聚合物材料種類繁多,假設材料庫中沒有相關材料資訊時,便要自行計算齒輪的強度。另外熱塑性材料的強度與溫度有關,因此在進行齒輪強度分析前應先推估齒輪工作溫度。因此本研究使用KISSsoft軟體輔助齒形設計,強度分析參考德國VDI-2736[1]標準計算聚合物齒輪的負載能力,透過與KISSsoft計算結果進行比對,提高計算的可靠度。
▋ 行星齒輪系設計
本研究使用行星齒輪系設計一減速機構,其機構簡圖如圖所示,圖中s為太陽輪,r為固定環齒輪,p為行星輪,X為行星臂架。首先根據限制條件如整體最大直徑和長度等,以及所需要的速比計算合適的齒輪參數,例如:齒數、模數及轉位係數等。由於使用的是熱塑性材料,溫度對於材料性質有很大的影響,因此必須計算齒輪的工作溫度,再進行強度分析,確保齒輪在運行中不會產生破壞,如果強度不足,則選擇是否要修改齒形設計或是更換材料。
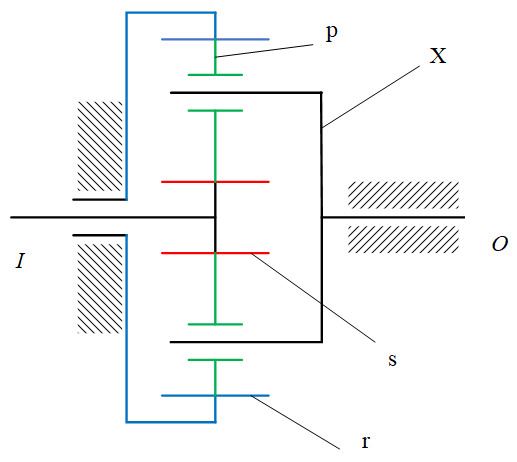
圖二、行星齒輪機構簡圖
假設太陽輪為輸入,環齒輪固定,行星臂架作為輸出,則行星齒輪系的減速比和太陽輪與環齒輪的齒數相關,可由下式計算:
其中,VR為減速比,(Zs)為太陽輪齒數,(Zr)為環齒輪齒數。當減速比越大時轉速越慢,輸出扭矩也隨之增加。
根據文獻[2, 3]在設計行星齒輪機構時,太陽輪齒數(Zs)、環齒輪齒數(Zr)、行星輪齒數(Zp)、行星輪個數(Np),要滿足同心條件、均勻分布條件與比鄰條件,以免發生干涉。
- 同心條件
在設計行星齒輪系時,太陽輪對行星輪以及行星輪對環齒輪之間的中心距必須相同,因此其齒數關係須滿足下式:
- 均勻分布條件
為了讓各行星輪之間所夾的角度相等,且與太陽輪嚙合時不會產生徑向負荷,因此太陽輪齒數加上環齒輪齒數,與行星輪的個數之間的比值要為正整數N,如下式所示:
- 比鄰條件
針對標準齒輪,為了不讓相鄰兩個齒輪產生碰撞,因此太陽輪齒數、環齒輪齒數、行星輪齒數,與行星輪個數之間的關係須符合下式:
若是轉位齒輪,行星齒輪外徑 需要滿足下式:
其中, 為太陽輪與行星輪間的中心距。
▋ 強度計算
本研究使用熱塑性材料,齒輪的工作溫度對於材料性質有很大的影響,因此必須先計算齒輪的工作溫度,再對齒輪進行強度分析,包含齒面接觸應力與齒根彎曲應力的評估,所需要的材料性質包含拉伸疲勞強度、滾動接觸疲勞強度、楊氏模數與浦松比。 參考德國VDI-2736[1]標準,可由下式計算齒輪的工作溫度:
其中,ϑFuβ 為齒輪溫度(°C), ϑ0為環境溫度(°C),P為馬達標稱輸出(W),μ為摩擦係數、Hv;為齒磨損程度,Kϑ,Fuβ為傳熱係數(K·(m/s)0.75·mm1.75/W),b為面寬(mm),z為齒數,Vt為切向速度(m/s),mn為模數(mm),Rλ,G為外殼的傳熱阻力(Km²/W),AG為外殼的散熱表面積(m²),ED為相對嚙合時間。
當齒頂受到應力時會導致齒根受到彎曲應力,可由下式得出:
其中,σF 為齒根彎曲應力(N/mm2),KF 為齒根負載係數,YFa 為齒形係數,YSa 為應力修正係數,Yε 為接觸比率係數,Yβ 為螺旋角係數,Ft 為切向力(N),bf 為有效面寬(mm),mn 為模數(mm),以上係數皆與齒形有關,並不受材料影響。σFP 為允許最大齒根彎曲應力(N/mm2),與材料的疲勞係數以及安全係數有關,可由下式計算:
其中,YSt 為應力修正係數,在計算聚合物齒輪強度時約等於 2,σFlimN 為材料拉伸疲勞強度(N/mm2),SFmin 為允許最小齒根安全係數
齒面接觸應力是基於兩齒輪相互嚙合時,齒面上的接觸點所承受的壓力,齒面接觸應力可由下式計算:
其中,±分別為齒輪外嚙合與內嚙合,σH 為齒面接觸應力(N/mm2),ZE 為彈性係數(N/mm20.5),ZH 為節點區域係數,Zε 為重合度係數,Zβ 為螺旋角係數,Ft 為切向力(N),KH為齒面載荷係數,bw 為工作面寬(mm),d1 為小齒輪直徑(mm),u 為齒數比。除了彈性係數(ZE)跟材料性質相關以外,其餘係數皆與齒形相關,彈性係數可由下式計算:
其中,ν為材料浦松比,E 為材料楊氏模數。
σHP 為允許最大齒面接觸應力(N/mm2),與材料性質和安全係數有關,可由下式計算:
其中,σHlimN 為滾動接觸疲勞強度(N/mm2),ZR 為表面粗糙度,在計算聚合物齒輪強度時約等於1,SHmin 為允許最小齒面安全係數。
▋ 數值範例
本研究使用的材料為POM,減速機構整體直徑為26 mm,馬達轉速為24500 rpm,額定扭矩為13 N-mm,減速機內不添加潤滑。目標將輸出扭矩提升至65 N-mm,所需要的減速比為5。根據設計條件設計的行星齒輪減速機構基本參數列於表,其中模數為0.6 mm,中心距為7.0 mm,太陽輪、行星輪與環齒輪齒數分別為9齒、13齒與36齒,根據公式(1)得到的減速比為5,滿足設計條件,內齒輪的齒根圓直徑為23.52 mm,加上壁厚可滿足減速機構整體直徑要求,圖為利用SOLIDWORKS繪製出的減速機構模型圖。
| 表一 行星齒輪系齒輪參數 |
| 參數 |
單位 |
太陽輪 |
行星輪 |
環齒輪 |
| 中心距 |
mm |
- |
7.0 |
- |
| 模數 |
- |
- |
0.6 |
- |
| 壓力角 |
deg |
- |
20 |
- |
| 齒數 |
- |
9 |
13 |
36 |
| 面寬 |
mm |
3.00 |
3.00 |
4.00 |
| 轉位係數 |
- |
0.47 |
0.32 |
-0.49 |
| 節圓直徑 |
mm |
5.40 |
7.80 |
21.60 |
| 齒頂圓直徑 |
mm |
7.02 |
9.23 |
20.10 |
| 齒根圓直徑 |
mm |
5.07 |
7.33 |
23.52 |
圖三、 減速機構模型圖
計算完齒輪參數,接著需先計算齒輪工作溫度,所需的參數如表所列,計算出的工作溫度約為25°C。本研究採用POM,其材料性質如表三所示,假設齒輪是長時間連續負載,循環次數為108,使用德國標準VDI-2736[1]計算齒根彎曲應力與齒面接觸應力的結果分別如表四與表五所示,經比較與KISSsoft計算結果相同。經過強度分析後,齒輪的安全係數皆超過1,由於在確認材料的性質時,負載循環次數選擇的是108,因此材料的強度會較低,若是在低負載的使用情形下,根據不同負載循環次數的多寡,以POM為例,最大強度會相差到2倍,代表齒輪更不容易損壞。
| 表二 工作溫度計算參數 |
| 參數名稱 |
符號 |
單位 |
數值 |
| 環境溫度 |
ϑ0 |
°C |
20.00 |
| 馬達輸出 |
P |
W |
33.35 |
| 摩擦係數 |
μ |
- |
0.28 |
| 齒廓損程度 |
HT |
- |
0.31 |
| 傳熱係數 |
kϑ,Fuβ |
K·(m/s)0.75·mm1.75/W |
2.10 |
| 切向速度 |
vt |
m/s |
6.93 |
| 外殼的傳熱阻力 |
Rλ,G |
Km2/W |
0.06 |
| 外殼的散熱表面積 |
AG |
m2 |
0.03 |
| 相對嚙合時間 |
ED |
- |
1.00 |
| 齒輪溫度 |
ϑFuβ |
°C |
25.00 |
| 表三 POM 在 25°C 下的材料性質 |
| 參數名稱 |
符號 |
單位 |
數值 |
| 拉伸疲勞強度 |
σFlimN |
N/mm2 |
34.30 |
| 滾動接觸疲勞強度 |
σHlimN |
N/mm2 |
22.80 |
| 楊氏模數 |
E |
N/mm2 |
2842 |
| 浦松比 |
v |
- |
0.44 |
| 允許最大齒根彎曲應力 |
σFP |
N/mm2 |
68.60 |
| 允許最大齒面接觸應力 |
σHP |
N/mm2 |
22.80 |
| 表四 齒根應力分析結果 |
| 參數名稱 |
符號 |
單位 |
太陽輪 |
行星輪 |
環齒輪 |
| 齒根負載係數 |
KF |
- |
1.00 |
1.00 |
1.00 |
| 齒形係數 |
YFa |
- |
2.63 |
2.65 |
2.63 |
| 應力修正係數 |
YSa |
- |
1.68 |
1.66 |
1.66 |
| 接觸比率係數 |
Yε |
- |
0.92 |
0.73 |
0.73 |
| 螺旋角係數 |
Yβ |
- |
1.00 |
1.00 |
1.00 |
| 切向力 |
Ft |
N/mm2 |
1.61 |
1.61 |
1.61 |
| 有效面寬 |
bf |
mm |
3.00 |
1.57 |
1.57 |
| 齒根彎曲應力 |
σF |
N/mm2 |
3.62 |
5.48 |
4.47 |
| 安全係數 |
SF |
- |
18.95 |
12.51 |
15.35 |
| 表五 齒面接觸應力分析結果 |
| 參數名稱 |
符號 |
單位 |
太陽輪 |
行星輪 |
環齒輪 |
| 彈性係數 |
ZE |
(N/mm2)0.5 |
23.68 |
23.68 |
23.68 |
| 節點區域係數 |
ZH |
- |
0.98 |
0.98 |
0.90 |
| 重合度係數 |
Zε |
- |
1.00 |
1.00 |
1.00 |
| 螺旋角係數 |
Zβ |
- |
1.00 |
1.00 |
1.00 |
| 螺旋角係數 |
kH |
- |
1.00 |
1.00 |
1.00 |
| 切向力 |
Ft |
N |
1.61 |
1.61 |
1.61 |
| 工作面寬 |
bw |
mm |
3.00 |
3.00 |
0.97 |
| 齒面接觸應力 |
σH |
N/mm2 |
19.77 |
19.77 |
18.51 |
| 安全係數 |
SH |
- |
1.15/td> |
1.15 |
1.23 |
▋ 結論
本研究透過KISSsoft軟體進行行星齒輪系的齒輪設計,根據德國標準VDI-2736[1]估算齒輪工作溫度並進行強度計算,包含齒根彎曲應力與齒面接觸應力,另與KISSsoft計算結果作比較,確認計算無誤,因此若軟體材料庫裡無選用的材料資料,可自行使用標準進行強度分析。除了強度分析之外,聚合物齒輪還必須要考慮到磨耗量,因為相比於一般的金屬齒輪,聚合物齒輪更容易受到磨損的影響,因此未來會向聚合物齒輪的磨耗量做進一步的探討。